Bài toán xếp hình | Huy's Blog
Tựa đề đầy đủ là "Bài toán xếp hình lên lá bài", mình đặt tiêu đề nửa vời vậy chỉ nhằm mục đích clickbait thôi :))

Trong bức hình trên là bộ bài Spot It!, gồm có 55 lá, mỗi lá có 8 hình vẽ khác nhau.
Điểm đặc biệt của bộ bài trên là: với 2 lá bài bất kì, sẽ luôn xuất hiện 1 hình vẽ giống nhau.
Vấn đề đặt ra là làm thế nào để ta có thể tạo ra một bộ bài với tính chất giống như bộ bài Spot It! ở trên?
Ta thử thu nhỏ phạm vi của đề bài lại như sau:
Sắp xếp 6 hình vẽ khác nhau vào một bộ bài gồm có 4 lá, mỗi lá có 3 hình.
Sao cho mỗi 2 lá bài bất kì thì sẽ có một hình vẽ giống nhau trên đó.

Bài toán nghe có vẻ rắc rối nhưng thật ra rất dễ để giải nếu quy về dạng một bài toán hình học cơ bản.
Đầu tiên, chú ý vào yếu tố 2 lá bài bất kì luôn xuất hiện 1 hình vẽ giống nhau. Trong hình học, đối tượng có tính chất tương tự như vậy chính là các đường thẳng.
2 đường thẳng bất kì không song song trên cùng một mặt phẳng thì luôn cắt nhau tại một điểm nào đó
Vậy ta có thể hình dung, mỗi lá bài sẽ là một đường thẳng, và giao điểm của 2 đường thẳng chính là hình vẽ giống nhau nằm trên 2 lá bài đó.
Theo đề bài chúng ta có 4 lá bài tương đương với 4 đường thẳng.
Mỗi lá bài có 3 hình vẽ suy ra chúng ta cần có 3 giao điểm trên mỗi đường thẳng.
Nếu ta vẽ 4 đường thẳng bất kì không song song như hình sau:
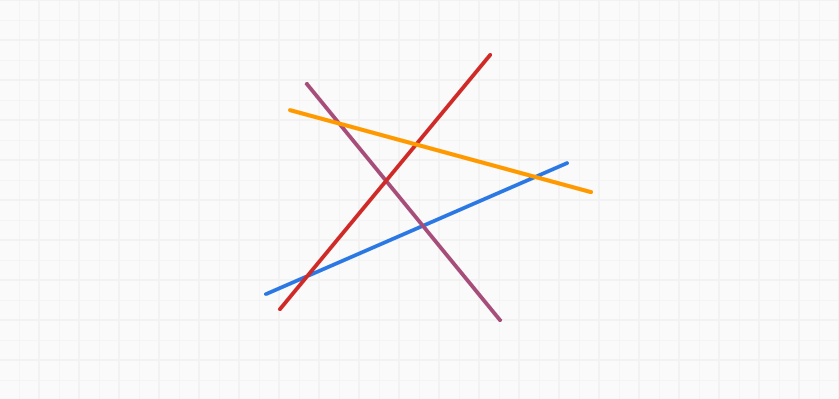
Ở mỗi giao điểm giữa các đường thẳng, ta đặt các hình vẽ trong đề bài vào:
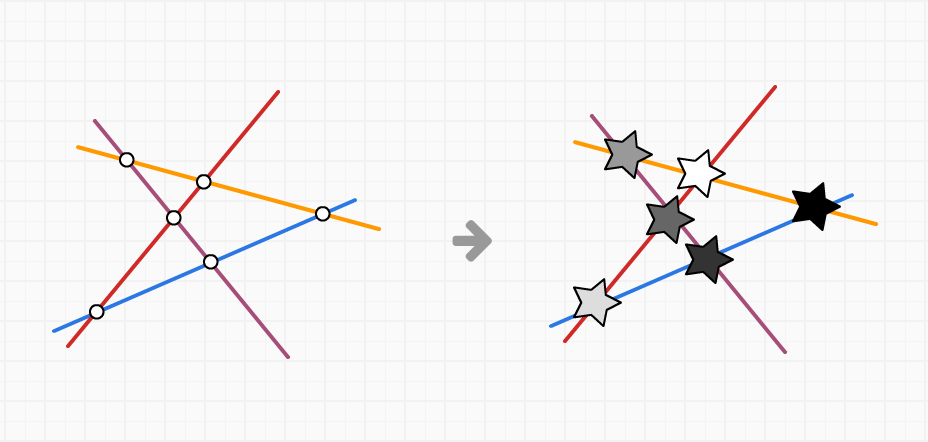
Như vậy các bộ 3 hình vẽ trên mỗi đường thẳng cũng chính là bộ 3 hình vẽ chúng ta cần đặt vào mỗi lá bài.
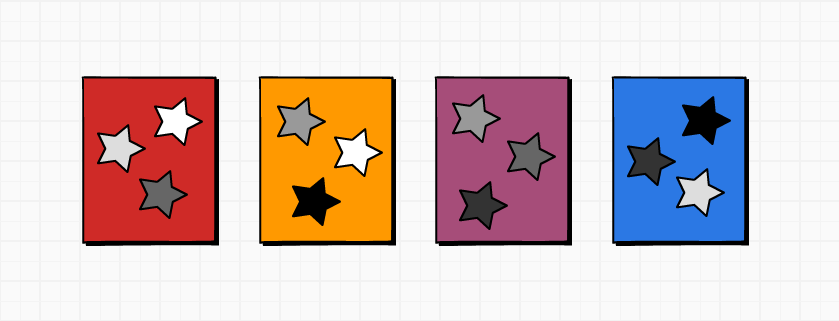
Quay lại bài toán ban đầu, để có thể tạo ra một bộ bài Spot It! với 55 lá bài và có 8 hình vẽ trên mỗi lá bài, chúng ta có thể vẽ 55 đường thẳng sao cho mỗi đường thẳng phải giao nhau với 8 đường thẳng bất kì. Và cần $(55 \times 8) / 2 = 220$ giao điểm, tương ứng với 220 hình vẽ.
Trích từ bài báo [The Intersection Game](http://www.maa.org/sites/default/files/pdf/horizons/PolsterApril2015.pdf), của Burkard Polster, đăng trên tạp chí Math Horizon, Hiệp hội toán học Hoa Kỳ (MAA), tháng 4/2015.